本文分为两部分
https://www.kabuku.co.jp/developers/anomaly-detect https://www.kabuku.co.jp/developers/time_series_anomaly_detect

異常検知の基礎(blog翻译)

关于异常检测的手法虽然多种多样，但是很少有日语的介绍，本文挑重点讲讲。

异常检测基本方法：

估计分布：从正常数据学习数据模型
定义异常度量：（偏移上述模型的距离？）
设定阈值：距离大于阈值就判断为异常

估计分布

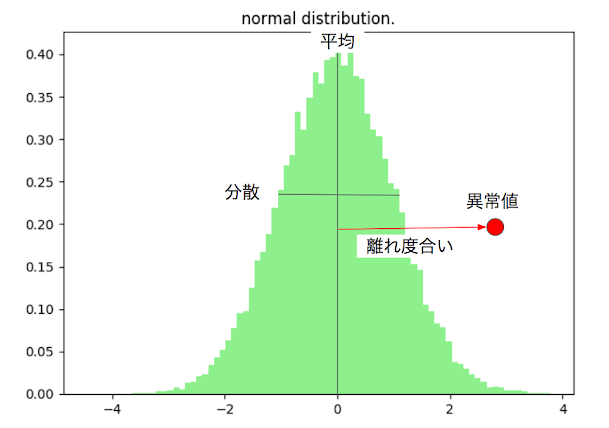
一般都用正态分布 $$ N(x|\mu,\sigma^2)=\frac{1}{\sqrt{2\pi}\sigma^2}exp(-\frac{1}{2\sigma^2}(x-\mu)^2) $$ 一般情况下$\mu=\frac{1}{N}\sum_{n=1}^{N}x_n, \quad\sigma=\frac{1}{N}\sum_{n=1}^{N}(x_n-\mu)^2$ 由于将正态分布定义为模型，并且均值和方差是从数据中导出的，因此适用于估计分布。

定义距离

通常采用负对数似然作为异常度量（距离）。例如我们通过负对数来计算观测值x'的异常度 $$ a(x')=\frac{1}{2\sigma^2}(x'-\mu)^2+\frac{1}{2}ln(2\pi\sigma^2) $$ 其中第二项与观测值无关，因此可以将它化简为 $$ a(x')=(\frac{x'-\mu}{\sigma})^2 $$ 以上是异常度的推导。在上式中，以样本均值为均值的正态分布中，通过将与均值的偏离程度除以标准差进行归一化。如图所示

设定阈值

最简单的阈值设定方法就是分位点。
例如2%分位点代表很少被观测到的数据，因此可以当作异常。

这个方法很简单，但是对比较分散的数据没有用。
这里介绍一种基于概率分布的阈值设定方法。
我们需要知道异常度遵循什么概率分布，根据Hotelling定理：

一维观测数据$D=x^{(1)},...,x^{(N)}$以及新观测数据x’分别独立且服从同一正态分布。
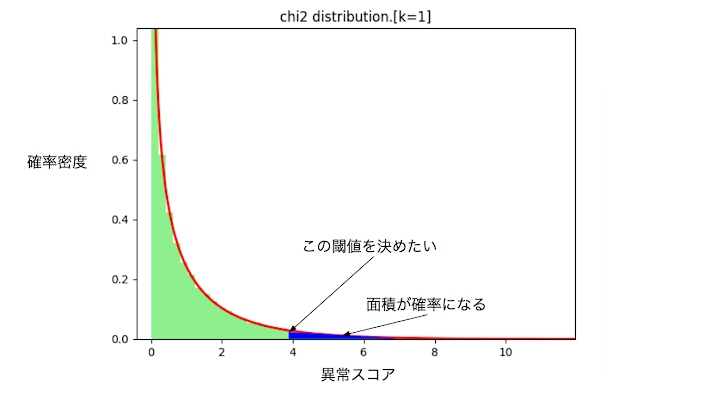
这时异常度$a(x')$的定数倍服从自由度为（1，N-1）的f分布，即 $$\frac{N-1}{N+1}a(x')\sim F(1,N-1)$$ 特别地，当N>>1时，$a(x')$服从自由度为1，scale因子1的卡方分布（カイ2乗分布） $$a(x')\sim \chi^2(1,1)$$

根据定理，异常度$a(x')$服从卡方分布，由此来设定阈值根据代码（详见原文），作图可知，定理是对的。

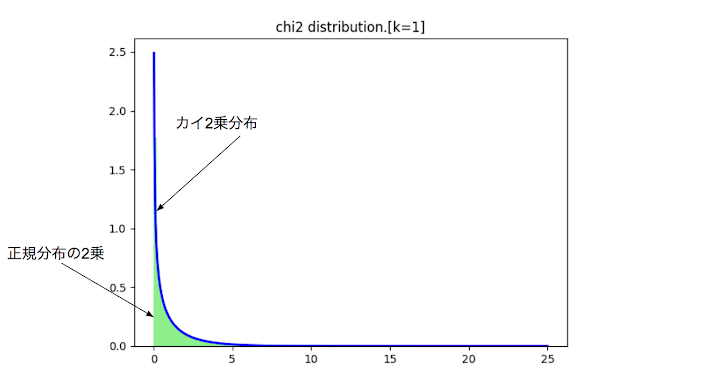
（众所周知，概率密度函数下面积为1，所以可以根据面积来定阈值）

接下来可以得到。。（懒得打公式了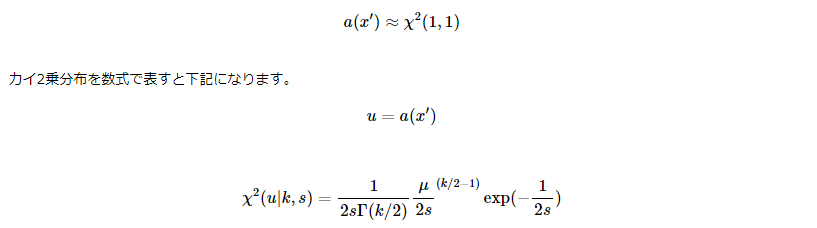）其中k是自由度，s是scale因子。根据这两个参数可以调整卡方分布面积的大小。

k=1,s=1时，卡方分布面积为1

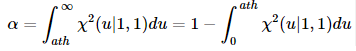
例如将α设置为0.01，则将得出异常分数的阈值ath，以使下图中的面积变为0.01。

最后举了一个例子，从csv里读数据，根据上述方法检测异常。具体代码详见原文，关键代码如下

() # 標本平均 mean = np.mean(data) # 標本分散 variance = np.var(data) # 異常度 anomaly_scores = [] anomaly_scores_dict = {} for x in data: anomaly_score = (x - mean)**2 / variance anomaly_scores.append(anomaly_score) anomaly_scores_dict.update({anomaly_score: x}) # カイ二乗分布による1%水準の閾値 threshold = stats.chi2.interval(0.99, 1)[1] for k, v in anomaly_scores_dict.items(): if k > threshold: print("anomaly weight {0} kg, anomaly score {1}".format(anomaly_scores_dict[k], k)) ()

時系列データにおける異常検知(blog翻译)

时间序列的异常检测与一般的异常检测相比，时间序列数据之间并不是独立的，而是有相互依存的关系。因此前文所提到的数据相互独立的假设不成立了，需要用到其他方法。
具有代表性的方法有以下几种。

动态时间伸缩法：简单但是处理不了噪声
特异光谱变换：能处理噪声但是计算开销大
自回归（AR）模型：能处理周期性数据，也可以用来做时间序列预测，变化点检测。但是由于次数p是确定的，除非状态恒定否则很难应用。
状态空间模型：可以处理状态变化，并且抗噪音。可用于时间序列预测和变化点检测，类似于自回归模型。但是较难处理周期性且稳定的数据。

接下来将针对AR模型和状态空间模型详细展开。

通过自回归模型进行异常检测是高度可扩展的，因为即使将预测模型替换为其他模型也可以使用
由于状态空间模型可以处理内部状态的变化，因此还可以检测状态变化的设备中的异常。示例：汽车传感器等