论文阅读-Estimating the number of unseen species: How many words did Shakespeare know?
Estimating the number of unseen species: How many words did Shakespeare know?
https://www.gwern.net/docs/statistics/1976-efron.pdf
概要
莎士比亚写过31534个不同的单词,其中14376个仅出现一次,4343个出现两次。本文所考虑的问题是推测他一共知道(但不一定使用)多少个单词。 我们试验了Fisher的参数经验贝叶斯模型和Good&Toulmin的非参数模型。 后一种理论使用线性编程方法进行了扩充。 我们得出的结论是,这些模型假设出了:莎士比亚至少还知道另外35,000个单词。
关键词:Empirical Bayes; Euler transformation; Linear programming; Negative binomial; Vocabulary
1 Introduction
估算未见物种的数量是生态研究中的一个常见问题。在本文看不见的物种是莎士比亚知道但没有使用的单词。根据xxx报告,莎士比亚的已知的作品共884647个词,其中14376个词只出现一次,4343词出现两次,846词出现100次以上,总共有31534个词被至少一次地使用。(具体计数见表格1)
注意本文中“type”,"word type"表示词的种类(重复出现只算一次),“total words”表示词出现的总次数。 “type”的定义是任何可区分的字母排列,因此“girl”和"girls"为不同type。
为了解决”莎士比亚实际上知道多少个单词类型?“这个问题,我们假设又发现了一个莎士比亚的著作集,包含884647*t个词。当t=1时,新发现的著作集词数量与原本的一样。根据Fisher, Corbet & Williams (1943)提出的参数化模型a parametric model以及Good & Toulmin(1956)提出的非参数化模型 a nonparametric model,答案是接近的,都是会新出现11460左右个新单词type。
当t为无穷大时,对应了最初提出的问题:莎士比亚知道多少个单词类型?我们会在第二章开头给出问题的明确数学定义。实际上这个问题没有可能的上限,但是根据我们推算出了下限至少为35000,即在原来已知的31534个词汇以外,莎士比亚还知道至少35000个词汇。
我们的推算是基于经验贝叶斯估计empirical Bayes estimation (Robbins, 1956; Good, 1953)。它还涉及计算和理论意义上的线性编程。 这种方法类似于Harris(1959)所采用的方法。相同标题的未发布报告提供了更多详细信息,可应要求从作者处获得。
2 THE BASIC MODEL
我们使用Fisher论文的物种捕获术语。假设存在S个物种,并且在一个单位时间后,我们已经捕获了$x_s$个物种s。 当然,我们只观察到那些大于零的值$x_s$。 基本的分布假设是,每个物种根据泊松分过程(泊松分布:平均一天卖$\lambda$个包子,那么每天卖出包子个数x的概率$P\sim Poisson(\lambda)$)进入陷阱(被捕获),即物种s单位时间被捕获的数量$x_s$服从均值(期望)为$\lambda_s(s=1,...,S)$的泊松分布。 本文中的大多数计算都不需要S个泊松过程相互独立。 每当需要独立性时,都会对其进行具体划分,并称为“独立性假设”。

(补充:
泊松分布: $$P(X=K)=\frac{\lambda^k}{k!}e^{-\lambda}$$泊松过程: $$P{N(t+s)-N(s)=n}=\frac{(\lambda t)^n}{n!}e^{-\lambda t}$$ 实验结果满足泊松分布的实验即为泊松过程。泊松过程把离散的伯努利过程变得连续化了:原来是抛n次硬币,现在变成了无穷多次抛硬币;原来某次抛硬币得到正面的概率是p,而现在p无限接近于0(p=lambda/n),即:非常难抛出正面朝上的硬币;但是n次实验中硬币朝上的次数的期望不变,即lambda恒定。在泊松过程中,我们把抛出硬币正面这样的事件叫做到达(Arrival)。把单位时间内到达的数量,叫做到达率(Arrival Rate)。 原文链接:https://blog.csdn.net/qq_34662278/java/article/details/84190456 )
图1给出了这种情况的示意图。我们可以从[-1, 0]的泊松过程 推断未来时间段t的泊松过程。令$x_s(t)$是整个时间段[-1, t]物种s出现的次数。这意味着:
- $x_s(t)$服从均值为$\lambda_s(1+t)$的泊松分布。(因为上文定义的$\lambda_s$是单位时间s出现均值,一共经历(1+t)时间长度)
- 在给定$x_s(t)$的情况下,x有条件地为二项式${x_s(t),1/(1+t)}$。(不懂为啥?)
对于在introduction描述的情况,t为新作品集中总词数除以884647.(因为回顾上文的假设:莎士比亚的著作集,包含884647*t个词。[-1, 0]表示已有的莎士比亚文集中的884647的单词)
其中第二点很关键。它实质上表示时间段[-1, 0]是整个时间段[-1, t]的典型值。
令$G(\lambda)$是$\lambda_1,...,\lambda_S$(S个物种分别在单位时间出现的期望值)的经验累积分布函数(empirical cumulative distribution function),并且$n_x$是所有物种在[-1, 0]时间段内被观测到x次的物种个数(例如图1中$n_1=1$为物种2,$n_{13}=1$为物种3),那么$n_x$的期望为
$$\eta_x=E(n_x)=S\int_0^\infty (\frac{\lambda^x}{x!}e^{-\lambda})dG(\lambda)$$
其中括号里为泊松分布的概率密度函数。
在莎士比亚例子中,$\eta_x$表示在已知的莎士比亚文集中出现x次的词汇个数$n_x$的期望。
令$\Delta (t)$为在时间段(0, t]被观测到,但是在[-1, 0]没被观测到的物种数量(即在原莎士比亚文集中没出现过,但是在未来可能出现的词汇),那么
$$\Delta (t)=S\int_0^\infty e^{-\lambda}(1-e^{-\lambda t})dG(\lambda)$$
(数学部分我还是不管了吧。。。)
经过变换,会发现
$$\Delta (t)=\eta_1t-\eta_2t^2+\eta_3t^3-...$$
这个有趣的结果被称为经验贝叶斯(empirical Bayes)
虽然它不一定收敛,但如果假设它收敛,那么就可以得出它的无偏估计,把莎士比亚的数据代入,得到t=1时,$\hat \Delta (1)=11430$(也就是说,如果莎士比亚再写884647个单词,将会有11430个新单词出现)
在独立性假设下,从保守角度出发,一个合理的近似值是将$n_x$自身作为独立的泊松变量,均值为$\eta_x$,在这种情况下此无偏估计的方差$Var{\hat \Delta (1)}=31534$,即它的标准差为178.
我们仅仅是通过统计量$n_1,n_2,...$来估计$\Delta(t)$,$n_0$实际上是不可观测的,和$\Delta(\infty)$一样。我们无视了与观测值$x_s$有关的标签。本文的估计量都是以这种形式,其他更好的方式有其他作者尝试,例如。。。
不过很可惜的是,上述$\Delta (t)=\eta_1t-\eta_2t^2+\eta_3t^3-...$的式子不适用于t>1,当t大于1时,随着项数的增加,$t^x$的几何增加的幅度会产生剧烈的振荡。Good&Toulmin建议使用Euler变换来强制该系列收敛。在第4章中会详细讨论这个想法。但是首先我们将在第三章中试验Fisher的参数经验贝叶斯模型Fisher's parametric empirical Bayes model
3 FISHER'S NEGATIVE BIOMIAL MODEL
Fisher在第二章提到的假设之外,又加了新的假设:
- 累积分布函数$G(\lambda)$可以被gamma分布的密度函数近似
- 参数$\lambda_1,...\lambda_S$独立且与假设1中的密度函数$g_{\alpha \beta}(\lambda)$同分布。
Fisher的假设1本身给出了该模型的大部分有用结论。每当引用假设2时,我们都会明确指出。假设1和2一起构成了Efron&Morris(1973)的参数经验贝叶斯模型a parametric empirical Bayes model。
(接下来的数学太特么难了,我选择放弃,反正就是推了一个参数化模型) 没有理由认为Fisher的参数模型将适合莎士比亚的数据。推荐它只是数学上的方便,并且在以前的经验上也很少。然而实际上,拟合度非常好。 在更改了参数$\hat \eta_1=14376$(仅出现过一次的词汇数,为何更改将在下面解释)后,$\hat \eta_x$变得十分接近$n_x$。为了评估如表2所示的拟合的准确性,我们需要一个误差理论,为此,我们既需要在第二章开头提到的独立性假设,也需要Fisher的假设2。考虑$n_x$的前$x_0$个元素$n_1,...,n_{x_0}$,假设它们的和为$N_0$,对于给定$N_0$,向量$(n_1,...,n_{x_0})$将服从多项式分布

表3显示了通过迭代搜索$x_0$的各种选择而获得的最大似然拟合。 最后一列是Wilks的似然比统计量,用于检验基于双参数模型的适当性。样本数量巨大,最小样本数为23517,因此在原假设下,该统计信息应作为卡方变量以$x_0-3$自由度分布。我们发现拟合度非常好,对于$x_0\leq15$来说甚至太好了。样本量如此之大,一般来说偏差仅为百分之几就会导致拒绝原假设。
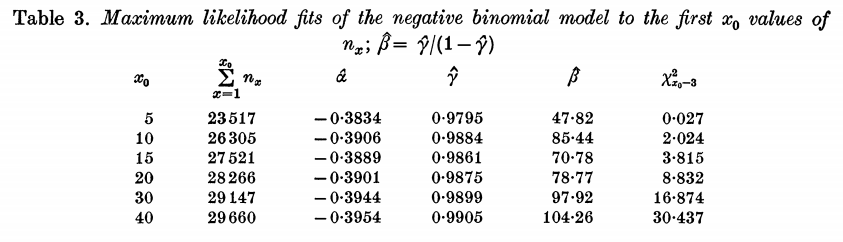
(接下来是一些关于选择参数的细节。。。)
虽然选择的参数$\hat\alpha=-0.3954$会导致t很大时$\Delta(t)$趋于无穷,不过,当t=1时,这个模型(对莎士比亚在包含884647的新作品集中有多少西南出现的单词)的估计值$\hat \Delta(1)=11483$.这与第二章的估计值只相差0.5%。
当t=10时,$\hat \Delta(10)=57704$,为现有莎士比亚作品集词汇数的两倍。那么这个结果准确吗?负二项式最大似然估计模型的假设标准误差(我们尚未计算)是没有信息的,因为我们知道该模型会在t很大时失效。因此我们在第4到7章寻找t很大时,对$\Delta(t)$的非参数估计,并评估准确性。
4 EULER'S TRANSFORMATION 欧拉变换
Bromwich提出的欧拉变换是一种强迫像第二章$\Delta(t)$的振荡序列快速收敛的方法。
(然后又是一堆数学公式)
这些公式表明如果要从$\hat \eta_x=n_x$计算$\hat\Delta$的话,$x_0$不能大于9.第五章的计算会表明$x_0=9$是一个合理的选择。相应的当$x_0=9$时,$\hat\Delta^9(1)=11441\pm147$,其中147是第五章计算出的结果。如果用$\hat\eta_x$的极大似然估计来计算$\hat\Delta^9(1)$, 它的值为11460.我们很难计算它的标准差,但是可以合理地说,该估计(11460)至少与第一个估计一样准确,甚至更加准确。
按照这样的表示方法,第二章的基本模型做出的估计可以表示成$\hat\Delta^\infty(1)=11430\pm178$。与上面的结果相比,我们把$x_0$从无限变成了9,因此减少了标准差的范围(从178降到147).不过根据xxx的记述,这是用偏差的代价换来的。$x_0$被截断到9,而不是无限,导致了它不是一个无偏估计。第五章的计算表明这个偏差可能从-62到+8。这里对于$G(\lambda)$的形式并没有做假设。在负二项式模型下,引理表明$\hat\Delta^9(1)$一定具有负偏差,因为我们忽略的所有项均为正。
因此如果我们将偏差和标准差都考虑进来,除了计算量之外,我们很难说$\hat\Delta^9(1)$的估计比原来第二章的$\hat\Delta^\infty(1)$估计要好。在计算t>1时,$x_0$的选择变得至关重要。我们将在第五章讨论。
5 GENERAL LINEAR ESTIMATORS 广义线性估计
这是欧拉变换的另一种表达形式,它能更加明显地影响振荡级数。
(又是一堆数学公式)

形如
$$\hat\Delta=\sum_{x=1}^\infty h_xn_x$$
被称为广义线性估计,我们用独立的泊松假设来计算这个估计的方差。这个值是通过作者的一个未公开报告计算得到的,它可能偏大。
(根据一堆计算)
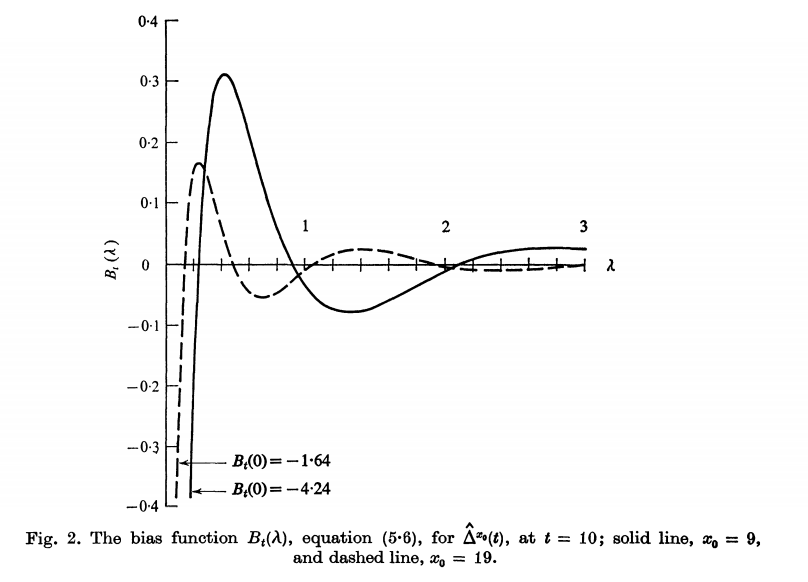
函数B表示估计$\hat\Delta$的偏差。例如取$t=1,x_0=9$时,(blablabla)其中估计的偏差[-62, 8]还没有用到表格1的信息,我们将在第六章和第七章用到这些信息来用更系统的方法计算边界。
如图分别是$t=9,x_0=9和19\infty$时的情况。。。(blablabla)相应的标准差变成$\hat\Delta^9(10)=45188\pm3994$以及$\hat\Delta^19(10)=53867\pm702566$.非常非常巨大的方差导致结果没有意义。从偏差与方差综合来看,$x_0=9$是更好的选择。
作者的未发表研究表明没有一个估计器明显好于$\hat\Delta^9(10)$
6 LOWER BOUNDS FOR $\Delta(t)$
随着t变大,估计$\Delta(t)$的合理上限变得越来越困难。假设莎士比亚实际上有$10^6$个单词类型,$\lambda_s=10^{-6}$,那么在我们上述模型下,预测将会很不准确。实际上当t没有那么大时,这个问题已经出现,上图图2中,t=10时,可能的负的偏差已经很大了。
不过估计下限将会比上限简单很多。
经过公式。。。线性估计器$\hat\Delta$将是$\Delta(t)$期望的下限。
表5显示了当$x_0=9$时,第五章的Euler估计器对于不同的t获得的下界。表5显示,随着t从10增长到120,$\Delta(t)$的这个合理保守的下界不会变得更大。 第七章将会表示,即使使用更通用的线性估计量,也无法获得接近于无穷大的t的更大的下界。这似乎表明,莎士比亚的数据不符合fisher的第一条假设,超出了t大于10的预测能力。
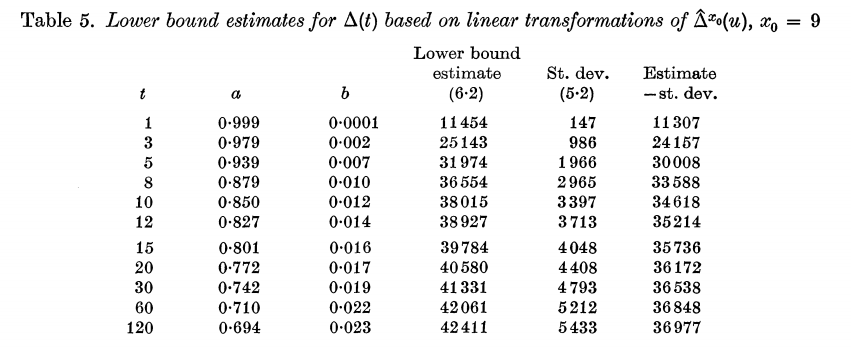
表5中的一个潜在缺陷是,忽略了a和b依赖于数据这一事实而得出了估计值和标准差,因为选择它们的目的是使(6.2)对于现有的数据集最大化。在这点上将在第七章考虑,结果显示没有太大的区别。
7 LiNEAR PROGRAMMING BOUNDS
第六章中寻找满足$E(\hat\Delta)\leq \Delta(t)$的$\hat\Delta$所使用的方法可以被泛化成一个线性规划问题a linear programming problem
提出了程序1.。。。基于一些实验,选定了一些参数在什么环境下做了计算。。。
。。。经过计算,对于$t=\infty$的情况,将所得的最佳系数h,代入公式(7.1),以获得莎士比亚的全部未观察词汇的下限估计$\hat\Delta(\infty)$= 59568。 不幸的是,在假设h为固定常数的前提下,根据公式(5.2)计算出的$\hat\Delta(\infty)$的标准误差是巨大的值204784。这似乎使$\hat\Delta(\infty)$毫无用处,但我们将看到, 实际上并非如此.
线性规划问题对程序1的对偶(Hillier&Lieberman,1974,p.90)或更确切地说离散化版本的对偶如下
推出了程序2.。。
对偶程序2找到了“最不利的情况”,程序2具有与程序1相同的答案。当$t=\infty$时,它给出了一样的59568。最小化分布G在5个相邻对中,10个$\lambda$值上有其支持,如表6所示。当然,我们不完全相信$\eta_x=\hat\eta_x$,但是我们可以放宽约束以考虑我们的不确定性.
根据两个公式,当$t=\infty,x_0=9, c=1$时,$\hat\Delta$的最小值为35554,这与表4的最后一栏非常一致。
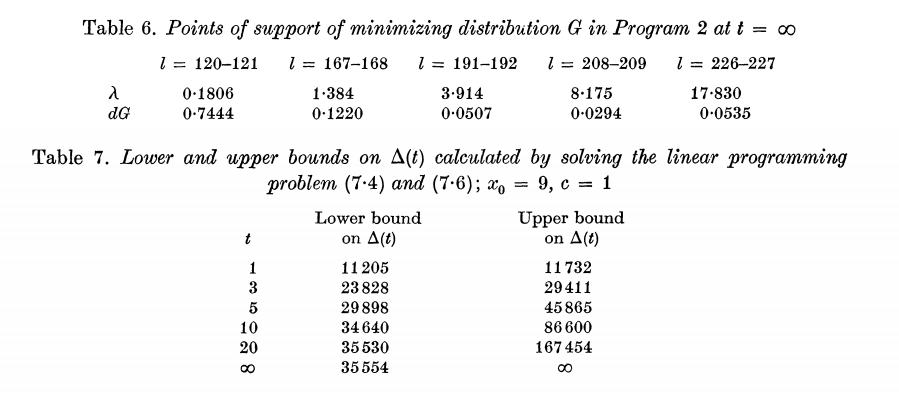
现在,我们对$\Delta(\infty)$有了一个令人信服的下限。选择c = 1似乎很乐观,但是我们有理由相信真实$\eta_x$比(2.6)表示的更接近$\hat\eta_x$。 我们在第六章关心的问题:从数据中选择估计量,然后在设置置信区间时忽略该选择过程的步骤,已经消失。线性规划方法根据未知参数$\eta_x$直接产生下界。$\eta_x$的置信界在$\hat\Delta$上产生边界。 对于那些更倾向于保守的界限的人,c=2给出了当$x_0=9$时,$\hat\Delta(\infty)$=30845。
表7给出了当$c=1, x_0=9$时获得的$\Delta(t)$的上下限。对于上限,只是将上式中的“最小化”简单地更改为“最大化”。表7所展示的下限与表5的最后一列的非常一致。 这很重要,因为表5比表7容易计算。
8 Conclusion
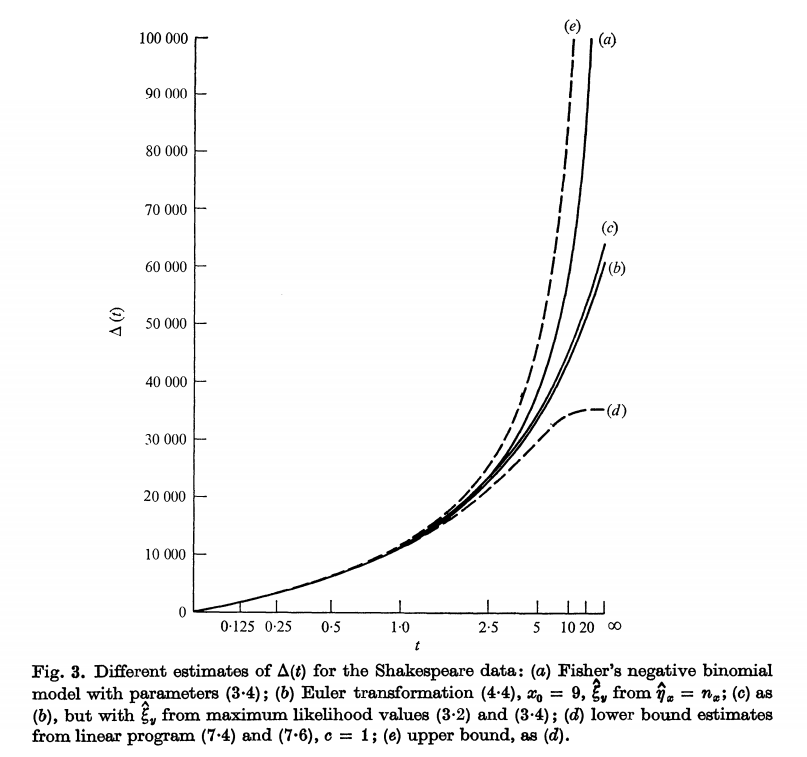
图3显示了$\Delta(t)$的不同估计。 我们对莎士比亚数据的经验总结如下。
- 估计$\Delta(t)$= 35000是莎士比亚知道但未使用的词汇量的合理保守下限。
- 对于$t\leq1$,可以非常准确地估算$\Delta(t)$,但是随着t的增大,不确定性会迅速放大。如果没有参数模型,则t大于10时,数据几乎不会提供其他信息。
- Fisher的负二项式模型非常适合该数据。但是,线性规划方法会产生其他经验贝叶斯解决方案,它们也适合观测数据,并且对于t>1时,给出较小的$\Delta(t)$估计。
- 对于t <1,所有方法都给出非常相似的答案
- 与更精细的技术相比,欧拉的变换效果很好
自己的分析
在第二章中,用到了贝叶斯定理(经验贝叶斯),这里所有单词出现的概率模型时基于泊松分布出现的。因此贝叶斯定理中的先验分布(以及后验分布)不是泊松分布,而是泊松分布模型中参数$\lambda$的分布,预测分布是预测新单词出现次数的分布(不像先验后验是参数的分布),因此是将算出参数的后验分布平均化后的分布。在本文第二章的具体问题中,作者没有给出泊松分布模型的参数$\lambda$的先验分布(没有针对参数作出假设,随便什么样的参数都可以),
其他
链接:https://www.zhihu.com/question/51952506/answer/226062437
1985年11月,一位美国学者Gary Taylor在英国牛津大学的一图书馆找到了一首诗(姑且称为“Taylor诗”好了),引发了一场英美研究莎士比亚文学作品的学者们的口水大战,争论的焦点就是此诗是否为莎士比亚所作。不少专家认为这首“Taylor诗”,不论是用字遣词,还是韵味风格,都迥异于莎士比亚其他作品。论战两个月后,1986年1月24日出版的Science 杂志刊登了一篇“莎士比亚的新诗:向统计学致敬”(Shakespeare's new poem: an ode to statistics)的文章,介绍两位统计学者Efron与Thisted如何以统计方法鉴定这首“Taylor诗”是否为莎士比亚所作的过程。Efron与Thisted的方法是这样的:每个人都有其各自的用字习惯,特别是对于生僻字,每个作者使用的习惯差异可能更大。在莎士比亚已知的总作品中,共有884,647个字,其中有31,534个相异字。这些相异字中,有14,376个字从头到尾只出现过1次,有4,343个字只出现2次。出现几次的字都被计算出来。那些在总作品中, 出现频率较低的,就是莎士比亚的生僻字。依据这些数据,假设这首共429个字的“Taylor诗”为莎士比亚所写,他们估计会有几个字,在总作品中从未出现(也就是新字),只出现1次,2次, ……,一直到曾出现99次,都给出估计值。实际情况与估计非常吻合。这样做还不够,会不会当时代的诗人用字习惯都差不多?于是,两人又找了三位大致与莎士比亚同时代的诗人,各取其一首诗,及另取四首莎士比亚的诗,与这首泰勒诗做比较。经过3种统计检定发现对前三首,若假设为莎士比亚的作品,罕用字出现次数之实际值与估计值皆不吻合。而所挑选的四首莎士比亚的诗,虽偶有不合,但总的来说是可接受的。Efron及Thisted说,他们的分析并无法完全证明“Taylor诗”为莎士比亚所写,但在罕用字之使用情况,如此与莎士比亚的总作品吻合,确实令人惊讶。一场文学上的争论,经统计学家发声后迅速平息,难怪要向统计学致敬了。运用统计方法来做决策,反映的是一种客观及合理的思维。与其主观的争论风格相同否,还不如以客观的统计方法来判定。但如何才算已经够客观?除了只检验“Taylor诗”外,Efron和Thisted还拿了几位与莎士比亚同时代的诗人来比较,这样做就更保险了。免得万一莎士比亚那个时期的诗人,有如时尚般,生僻字之使用习惯类似,则此检定就没有什么参考价值了。统计正如我们的思维,客观至上,否则便是自欺欺人。反之我们的思维若是统计式的,便是极客观的。