情報学習論レポート サッカーリーグの順位推定

情報学習論レポート

Yasuhiro
June 27 2020

動機付け

2020年初め、新型コロナの影響で、スポーツを含めて様々なイベントは中止しなければならない状態で、私がいつも見てるイングランドのサッカーリーグ「Premier League」も38節380試合中、29節287試合(3試合は時間調整)だけが行われて中止になりました。 新型コロナの影響がますますがますます大きなるにつれて、Premier Leagueが今シーズン再開できなくなる心配もありますが、リーグの順位結果は来年のチャンピオンズリーグの資格(前四位)につながります。

もし再開できない場合、それに対して二つの計画が提案されました： 1.今シーズン全部キャンセル、チャンピオンズリーグの資格は去年と同じにする。 2.今の順位表のままで、チャンピオンズリーグの資格を決める 多くの人が二番目の提案に賛成するが、この方法では以下の問題があります： 1.試合が時間調整の原因で行わなかったので、今の順位表の20チームの内、6チームが27試合で、14チームが28試合を行った状況である。順位表の決定方法は勝ち点は勝利3点、引き分け1点、敗北0点で、勝ち点が多い順に順位を決めている。このまま計算すると、6チームに不公平。 2.日程によって、残りの試合の相手の強さは違う。

このレポートは以上の問題を解決するために、数理的な方法で中止したリーグの順位を決めることが目的です。具体的に、20チームがお互いにホームとアウェイで試合をする、380試合が行われた時と同じように、287の試合結果からチームの順位を決めます。

データセット：

試合結果は様々なウェブサイトから見られますが、まとめられたファイルがないので、今回はBBCスポーツ https://www.bbc.com/sport/football/premier-league/scores-fixtures/ から試合結果をクローラーで取得しました。クローラーの詳細はhttps://github.com/yasuhiro0802/Soccor-team-ability-estimator/blob/master/get_scores.py で参照してください。

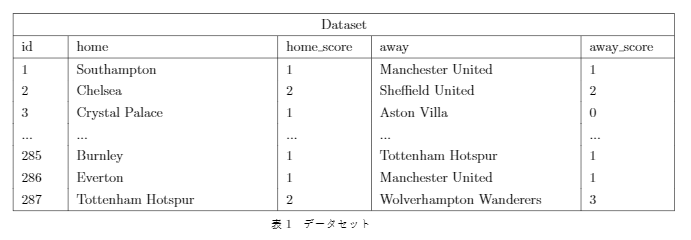
データは表1のように、home, home_score, away, away_score四つのコラムで、homeとawayはチーム名で、home_scoreとaway_scoreは試合の得点です。

問題の定式化

仮説：

サッカー試合を分析してチームの実力を計算するのはとても複雑な問題なので、簡単のため以下の仮説を置きます。

• チームの実力は攻撃力を示す$\alpha$と防御力を示す$\beta$の足し合わせとして考える。
• 各チームの$\alpha$と$\beta$は全シーズン固定とする。つまり、メンバーのローテーション、状態、監督の戦術、ホームかアウェイかなどは考慮しない。
• 試合で得点する確率は得点側の攻撃力$\alpha$と相手側の防御力$\beta$だけが関係する。
• 毎試合の時間は90分で固定とする。
• 各試合は独立で、試合中両方の得点も独立とする。

定式化：

リーグに参加したチームはチーム1, チーム2, ... , チームNと呼びます。チームiの攻撃力は$\alpha_i$、防御力は$\beta_i$と表します。

チームiとチームjの試合で、チームiが得点する確率ｐは、仮説の通り、チームiの攻撃力$\alpha_i$およびチームjの防御力$\beta_j$だけで決まります。チームiの攻撃力が高いほど、チームｊの防御力が低いほど、チームiが得点する確率が高くなります。これより様々な関係式が考えられます、例えば $p\propto (\alpha_i - \beta_j)$、$p\propto \frac{\alpha_i}{\beta_j}$です。

サッカーにおける得点はポアソン分布に従うことが知られています。ポアソン分布を表す確率関数は以下の通りです。 $$P(k|\lambda)=\frac{\lambda^k e^{-\lambda}}{k!}$$

単位時間あたり平均 λ 回起こるようなランダムなイベントが，単位時間にk回発生する確率がP(k)です。サッカーの場合には、90分(単位時間)内平均λ回の得点が、90分内にk回得点する確率がP(k)です。簡単のため、チームiがチームjから得る得点の平均を $$\lambda = \alpha_i - \beta_j$$ とします。

1試合のホームチームの得点をx、アウェイチームの得点をyとします。ホームチームはチームi、アウェイチームはチームjとします。チームiが90分内でアウェイチームのチームjからx点取、チームjが90分内でホームチームのチームiからy点取った場合を考えます。試合中両方の得点が独立だという仮説にしたがって、t番目の試合結果の確率は $$P((x,y)^{(t)}) = P(x^{(t)}|\alpha_{j^{(t)}},\beta_{i^{(t)}}) \cdot P(y^{(t)}|\alpha_{i^{(t)}},\beta_{j^{(t)}})$$ を表せます。$x^{(t)}$, $y^{(t)}$, $i^{(t)}$, $j^{(t)}$はそれぞれホームチームの得点数、アウェイチームの得点数、 ホームチームの番号、アウェイチームの番号です。

解析手法

今回の目標はT個の試合結果から、Nチームx2のパラメータを推定することです。用いる手法は最尤推定です。 尤度函数は $$L(\Theta)=\prod_{t=1}^T P((x,y)^{(t)})$$ 式を代入すると $$L(\Theta)=\prod_{t=1}^T \frac{(\alpha_{j^{(t)}}-\beta_{i^{(t)}})^{x^{(t)}}(\alpha_{i^{(t)}}-\beta_{j^{(t)}})^{y^{(t)}} e^{(-\alpha_{i^{(t)}}-\alpha_{j^{(t)}}+\beta_{i^{(t)}}+\beta_{j^{(t)}})}}{x^{(t)}!y^{(t)}!}$$ 尤度の負の対数は $$E(\Theta) = -\ln L(\Theta) = \sum_{t=1}^T [(-\alpha_{i^{(t)}}-\alpha_{j^{(t)}}+\beta_{i^{(t)}}+\beta_{j^{(t)}})+x^{(t)}\ln(\alpha_{j^{(t)}}-\beta_{i^{(t)}})+y^{(t)}\ln(\alpha_{i^{(t)}}-\beta_{j^{(t)}})-\ln(x^{(t)}!y^{(t)}!)]$$

となります。この関数を最小化するため、勾配法を使います。$\tau$は訓練回数を表します。 $$\alpha^{(\tau+1)} = \alpha^{(\tau)}-\eta \frac{\partial E}{\partial \alpha}$$ $$\beta^{(\tau+1)} = \beta^{(\tau)}-\eta \frac{\partial E}{\partial \beta}$$

m番目のalphaとの勾配は

$$\frac{\partial E}{\partial \alpha_m} = \sum_{t=1}^T (I(i^{(t)}=m) \cdot (\frac{y^{(t)}}{\alpha_{i^{(t)}}-\beta_{j^{(t)}}}-1) + I(j^{(t)}=m) \cdot (\frac{x^{(t)}}{\alpha_{j^{(t)}}-\beta_{i^{(t)}}}-1))$$

となり。同じく、n番目の$\beta$との勾配は $$\frac{\partial E}{\partial \beta_n} = \sum_{t=1}^T (I(j^{(t)}=n) \cdot (1-\frac{y^{(t)}}{\alpha_{i^{(t)}}-\beta_{j^{(t)}}}) + I(i^{(t)}=n) \cdot (1-\frac{x^{(t)}}{\alpha_{j^{(t)}}-\beta_{i^{(t)}}}))$$

となります。ただし、Iは指示関数です。

実例

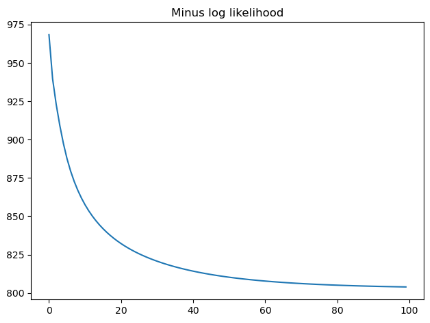
第2章のデータに対して第3章で取り上げたモデルを適用し、その訓練結果を図で表します。

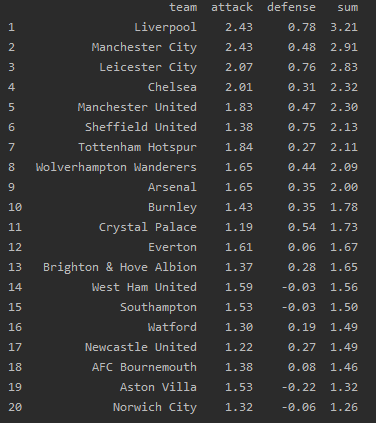
推定した各チームの$\alpha$と$\beta$とその足し合わせを図2で表します。

考察と展望

考察

2020年3月に中止したプレミアリーグの順位表を図3に示します。

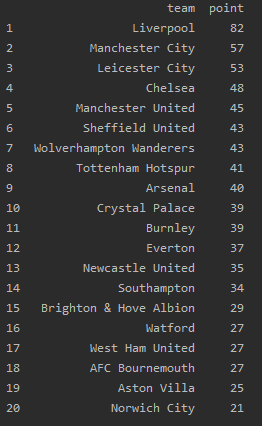
図3の順位は図2の推定結果と比べて少し異なります。その原因は第一章で記した順位表からそのまま実力を推定することによる問題点だと考えられます。

展望

本レポートでは、簡単のため第二章で複数の現実と離れた仮説を置いた上で順位表を得ました。現実に合わせるために、より複雑なモデルを考えなければなりません。例えば試合中の両チームの得点の関係、メンバーのローテーション、同じチームのホームとアウェイでの戦力差などを考える必要があります。

追記

2020年6月でプレミアリーグが無事に無観客で再開されました。しかし、このレポートは無意味だったわけではありません、同じ手法で他の問題への応用することもできます。例えばシーズン最後の順位を推測することや1試合の結果の予測することなどが考えられます。

ozuminと楯くんから貴重な意見をもらい、心から感謝申し上げます。